Covariance and Correlation Math 217 Probability and Statistics Prof D Joyce, Fall 14 Covariance Let Xand Y be joint random variables Their covariance Cov(X;Y) is de ned by Using formula, (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zx Then, x = a y = b z = 1 (a – ()b 1) 2 = a 2 b 2 1 2 2 x }a x b 2 x b x 1 2 x 1 x a = a 2 b 2 1 – ab – b a Question 5 Factorize (i) 4x 2 9y 2 16z 2 12xy – 24yz – 16xz Solution Using formula, (x y z) 2 = x 2 y 2 z 2 2xy(x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a Example 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2 2·2·5 (2a) 2 = (5 2a) 2 Consequences of the above formulas (x y) 2 = (y x) 2 = y 2 2xy x 2 (x y) 2 = ((x y)) 2 = (x y) 2
If X Y 3 And X Y 185 What Is X And Y Quora
The identity x 2 y 2 2 x 2-y 2 2 2xy 2
The identity x 2 y 2 2 x 2-y 2 2 2xy 2-Problem 2 Determine the global max and min of the function f(x;y) = x2 2x2y2 2y2xy over the compact region 1 x 1; If 2cos theta sin theta = x and cos theta 3sin theta = y ( Prove that 2 x sq y sq 2xy = 5 )Plz answe Get the answers you need, now!



Does Sqrt X 2 Y 2 X Y Brilliant Math Science Wiki
1 Let f(z) = y 2xyi( xx2 y2)z2 where z= xiyis a complex variable de ned in the whole complex plane For what values of zdoes f0(z) exist? 1 The trivial inequality a 2 ≥ 0 is true for any a Im particular, it must be true that ( x − y) 2 ≥ 0 But, ( x − y) 2 = x 2 − 2 x y y 2 Therefore, the result follows Share answered Oct 7 '18 at 708 JamesX=y The equation is now solved Solutions are the same y^{2}2xyx^{2}=0 All equations of the form ax^{2}bxc=0 can be solved using the quadratic formula \frac{b±\sqrt{b^{2}4ac}}{2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction
80 Given that xy=12 and xy = 32 Using the identity, (xy) 2 = x 22xyy 2 ⇒ (12) 2 = x 264y 2 ⇒ 144 = x 2y 264 ⇒ 144−64 = x 2y 2 ⇒ 80 = x 2y 2 The answer is x 2y 2 = 80For example, the identity (x y) 2 = x 2 2 x y y 2 (xy)^2 = x^2 2xy y^2 (x y) 2 = x 2 2 x y y 2 holds for all values of x x x and y y y Since an identity holds for all values of its variables, it is possible to substitute instances of one side of the equality with the other side of the equalityCalculus Basic Differentiation Rules Implicit Differentiation
Partial Differential Equations Exam 1 Review Solutions Spring 18 Exercise 1 Verify that both u= log(x2y2) and u= arctan(y=x) are solutions of Laplace's equation u xx u yy= 0 If u= log(x2 y2), then by the chain rule u x= 2x x 2 y) u xx= (x2 y2)(2) (2x)(2x) (x 2 y) 2y2 2x2 (x y2)2 and by the symmetry of uin xand y, Use the Pythagorean identity (x2 y²)2 (2xy)2 = (x2 y2)2, to create a Pythagorean triple Follow these steps 1 Choose two numbers and identify which is replacing x and which is replacing y 2 How did you know which number to use for x and for y 3 Explain how to find a Pythagorean triple using those numbers 4(x 3) (x – 3) = x 2 – 3 2 = x 2 – 9 Problem Solve (x 5) 3 using algebraic identities
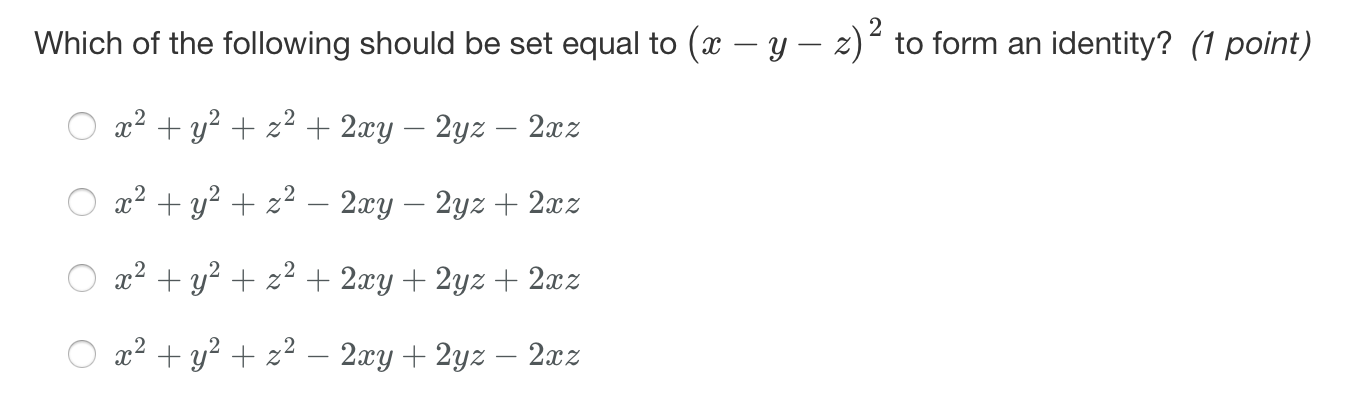



Solved Which Of The Following Should Be Set Equal To X Y Chegg Com




Teaching Note Supply Tiles For Students A Apr 4 Objective Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example Ppt Download
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the square of a binomial, etc(c) u(x,y) = sinxcoshycosxsinhy Solution (a) If u(x,y) = x2y2, then u xxu yy = 22 = 4 6= 0 Therefore u(x,y) = x2y2 is not a solution (b) If u(x,y) = ln(x2 y2)3/2 = 3 2 ln(x2 y2), then we get u x = 3x x2 y2, u y = 3y x2 y2, u xx = 3 −x2 y2 (x2y2)2, u yy = 3 x2 −y2 (x2 y2)2Powers of 3 value 3^1 1/3 3^0 Jess owns 4 red shirts, 5 blue shirts, and 3 white shirts




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Darius Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show That 9 81 What Values Can Darius Brainly Com
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicFind dy/dx x^2y^2=2xy Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of with respect to is Differentiate using the Power Rule which states that is whereIf you mean x^2 y^2 X^2Y^2 can be written as (xy)(xy) Afterwards you substitute xy with 10 So now you are at 10(xy)=1 so xy = 12 After that, given xy= 12 and xy= 10, we do (xy)(xy)= 12–10 that gives us xyxy=2 then 2y=2 so y=1 then you do (xy) y= 12–1 So lastly x= 11 ( That verifies x^2 y^2= 1 121–1=1 and xy= 11–1=10)




Polynomials Ppt Video Online Download




Generate Pythagorean Triples Using An Identity Learnzillion
(b) u(x,y) = ln(x2 y2)3/2; The equation of a circle is x^2 y^2 – 12y = 0 What are the coordinates what is the patern in the values as the exponents increase?= (5a) 2 (2b 7c) 2 Using identity (x y) 2 = x 2 2xy y 2, considering x = 2b and y = 7c = 5a (2b 7c)5a (2b 7c) Using identity x 2 y 2 = (x



Double Integrals Over General Regions Calculus Volume 3



If X Y 3 And X Y 185 What Is X And Y Quora
(b) 3 binomials with x and y as variables;(y2 2xy)dx− x2dy = 0 we have M(x,y) = y2 2xy and N(x,y) = −x2, which leads to ∂M ∂y = 2x2y and ∂N ∂x = −2x Since ∂M ∂y 6= ∂N ∂x the equation is not exact However, 1 M ∂N ∂x − ∂M ∂y = − 2 y which implies that thereexists an integratingfactor, dependingonly on y, which satisfies 1 µ dµ dy = − 2 y AnX and y are positive integers;
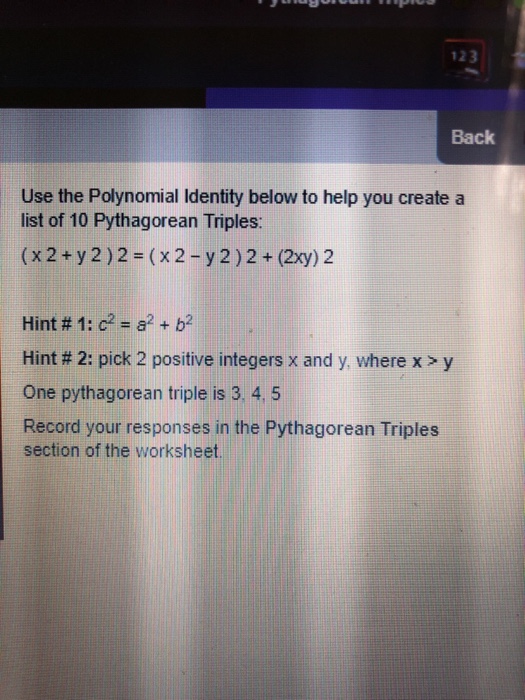



Solved 123 Back Use The Polynomial Identity Below To Help Chegg Com




Lagrange Multipliers Ppt Download
(c) 3 monomials with x and y as variables;Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as;




Jason Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show That 6 36 Brainly Com




4 08 Polynomial Identities And Proofs By Sheila Bartlett
Free PDF download of NCERT Solutions for Class 8 Maths Chapter 14 Exercise 142 (EX 142) and all chapter exercises at one place prepared by expert teacher as per NCERT (CBSE) books guidelines Class 8 Maths Chapter 14 Factorisation Exercise 142 Questions with Solutions to help you to revise complete Syllabus and Score More marks Register and get all exercise solutions in your emails To find the value for Solution Let's consider x = 2 and y = 3 and solve the equation hence proved The formula for mitgliedd1 and 1Verify Stokes' Theorem for the field F = hx2,2x,z2i on the ellipse S = {(x,y,z) 4x2 y2 6 4, z = 0} Solution We compute both sides in I C F·dr = ZZ S (∇×F)·n dσ S x y z C 2 1 1 2 We start computing the circulation integral on the ellipse x2 y2 22 = 1 We need to choose a counterclockwise parametrization, hence the normal to




Polar Coordinates Ppt Download




Expand Each Of The Following Using Suitable Identities 2x Y Z 2
How do you use Implicit differentiation find #x^2 2xy y^2 x=2# and to find an equation of the tangent line to the curve, at the point (1,2)? Explanation For x2 y2 = 2xy, we get (by differentiating implicitly), dy dx = 1 That's the same as the derivative of a linear function with slope, 1 Hmmmmm Let's see and dy dx = 1 (Which we already knew by differentiating, but this may be of interest as well)(d) 2 polynomials with 4 or more terms




X 2 Y 2 16 2xy 8x 8y Factorise Using Suitable Identity Brainly In




Chapter 3 More About Factorization Ppt Download
Multiply \frac {y^ {2}2xyx^ {2}} {x^ {2}y^ {2}} times \frac {2x} {xy} by multiplying numerator times numerator and denominator times denominator Cancel out x in both numerator and denominator Factor the expressions that are not already factored Cancel out xy in both numerator and denominatorAlgebra Factor x^22xyy^2 x2 2xy y2 x 2 2 x y y 2 Check that the middle term is two times the product of the numbers being squared in the first term and third term 2xy = 2 ⋅x⋅y 2 x y = 2 ⋅ x ⋅ y Rewrite the polynomial x2 2⋅x⋅yy2 x 2 2 ⋅ x ⋅ y y 2Medium View solution > The area of a square is 9 x 2 2 4 x y 1 6 y 2 Find the side of the square Medium View solution > View more



What Are The Asymptotes Of The Curve X 2y 2 X 2 Y 2 2 X 2 Y 2 3 0 Quora




Ppt Polynomials Powerpoint Presentation Free Download Id
Putting a = 04p & b = 05q = 016p 2 – 04pq 025q 2 (vi) (2xy 5y) 2 Solution (2xy 5y) 2 Using Formula (a b) 2 = a 2 b 2 2ab Putting a = 2xy & b = 5y = (2xy) 2 (5y) 2 2 (2xy) (5y) = 4x 2 y 2 xy 2 25y 2 Question 4 SimplifySolution Our plan is to identify the real and imaginary parts of f, and then check if the CauchyRiemann equations hold for them We have f(z) = y 2xy i( x x2 y2) x2 y2 2ixy = x2 2xy y y2 i( xConstruct (a) 3 binomials with only x as a variable;



1



Solved Solve The System X 2 Y 2 15 Xy 5 Y 0 Select One 5 5 2 5 5 2 B 5 5 2 5 5 2 C This System Is Dependent D No So Course Hero
Get FREE NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 25 We have created Step by Step solutions for Class 9 maths to help you to revise Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given (i) Area 25a2 – 35a 12 (ii) Area 35y2 13y – 12 Solution (i) We have, area of rectangle = 25a 2 – 35a12 = 25a 2 – a – 15a12Put the values of v which you let in point 2 and you will get your answer Now lets do the math Given that (x^2 y^2)dx 2xy dy =0;




Differential Calculus Concepts Problems 126 Rd 1 Matrix




Ex 2 5 3 I Factorise 9x2 6xy Y2 Using Appropriate Identities
0 y 2 Solution We look for the critical points in the interior(a) u(x,y) = x2 y2;Solution for x^22xyy^2=0 equation Simplifying x 2 2xy y 2 = 0 Reorder the terms 2xy x 2 y 2 = 0 Solving 2xy x 2 y 2 = 0 Solving for variable 'x' Factor a trinomial (x 1y)(x 1y) = 0 Subproblem 1 Set the factor '(x 1y)' equal to zero and attempt to solve Simplifying x 1y = 0 Solving x 1y = 0 Move all terms containing x to the left, all other terms to the right



Does Sqrt X 2 Y 2 X Y Brilliant Math Science Wiki




Solved 2 Pdf Identity Crisis Worksheet 4 Use The Chegg Com
Y (a2) Shrinking radial eld x y (a3) Unit tangential eld 2 De nition and computation of line integrals along a parametrized curve Line integrals are also calledpath or contour integrals We need the following ingredients A vector eld F(x;y) = (M;N) A parametrized curve C r(t) = (x(t);y(t)), with trunning from ato bDy/dx= (x^2 y^2)/ 2xy ( Homogenous) 1 f(x,y)= (x^2 y^2)/2xy, f ( kx,ky) = {(kx)^2 (ky^2)}/ 2kx ky = {(x^2 y^2)/2xy} k=0 (zero degree) Put y= vx =>dy/dx= v dv/dx 2 By 1 and 2 equation we get,Answer (x2 y2) = (x y)2 – 2xy or (x – y)2 2xy Consider the equation (x y) 2 = x 2 y 2 2xy (1) (x – y)2 = x 2 y 2 – 2xy (2) From equation (1) x2 y2 = (x y)2 – 2xy x2 y2 = (x – y)2 2xy




If X Y 2 2 X 2 Y 2 And X Y Lambda 2 4 Lambda 0 Then Lambda Is Equal To




Solved 2x Y 52 8 3 2y 2 10 41 Y 42 23 3c Y 1 1 I Y 7 21 3y
X x2 y2 − i y x2 y2, (211) whose real and imaginary parts are graphed in Figure 1 Note that these functions have an interesting singularity at the origin x= y= 0, but are harmonic everywhere else A slightly more complicated example is the function f(z) = z−1 z1 (212)Show activity on this post One (simple) way let t = x 2 y 2 xy then t xy ≥ 0 since it is the sum of two real squares x 2 y 2 and t xy ≥ 0 since it is the square of the real (x y) since (x y) 2 = x 2 y 2 2xy adding these, we get 2t ≥ 0, therefore t ≥ 0 Share Find dy/dx if x^2y^2=2xy A x/(xy) B (yx)/(yx) C 1 D x/y E None of these algebra The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;




View Question A Student Is Asked To Calculate The Pythagorean Triples For The Number 13 Using The Identity X 2 Y 2 2 2xy 2 X 2 Y 2 2 The Student S Steps Are




Solved What Is An Identity 1 Point An Identity Is A False Chegg Com
Ex 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xyNCERT Solution For Class 9 Maths Chapter 2 Polynomials Using identity, (xyz)2 = x2y2z22xy2yz2zx Here, x = (1/4)a y = (1/2)b z = 1 5 Factorize (i) 4x29y216z212xy–24yz–16xz (ii) 2x2y28z2–2√2xy4√2yz–8xz SolutionGenerate Pythagorean Triples using an identity You'll gain access to interventions, extensions, task implementation guides, and more for this video In this lesson you will learn to generate a Pythagorean Triple by using the identity (x^2 y^2)^2 (2xy)^2 = (x^2 y^2)^2




Algorithm For X 2 Xy Y 2 Z 2 With The Solution 1 1 1 That Download Scientific Diagram




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Exercise 6 5 Get Free Pdf
Tangent of x^22xyy^2x=2, (1,2) \square!Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music




Multiply X 2 4y 2 Z 2 2xy Xz 2yz By X 2y Z




A Apr 4 Objective Adding Amp Subtracting Polynomials Prove Polynomial Identities And Use Them




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube




Ppt Polynomials Powerpoint Presentation Free Download Id




If Sin 2 Z X 2 Y 2 1 2x Then X Must Be The Equation Sin 2 Z Askiitians




Algebric Identity X2 Y2 X Y X Y Youtube



Darius Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show That 9 81 What Values Can Darius Brainly Com
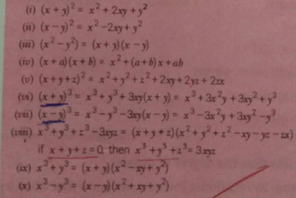



I X Y 2 X2 2xy Y2 Ii X Y 2 X2 2xy Y2 Iii X2 Scholr



How To Factorise Math Yz 2 Xz 2 Y 2z X 2y X 2z Xy 2 2xyz Math Quora




Use The Pythagorean Identity X2 Y 2 2xy 2 X2 Y2 2 To Create A Pythagorean Brainly Com



Solved Part 1 Pick A Two Digit Number Greater Than 25 Rewrite That Two Digit Number As A Difference Of Two Numbers Show How To Use The Identity Course Hero




Geometrically Verify The Identity X Y 2 X 2 Y 2 2xy




Ppt Polynomials Powerpoint Presentation Free Download Id



How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora
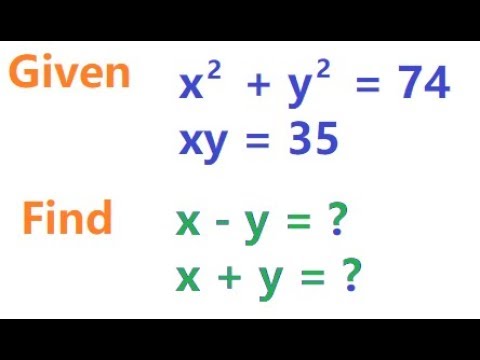



X 2 Y 2 74 And Xy 35 Find X Y And X Y 2x 3y 14 And Xy 8 Find 4x 2 9y 2 Youtube




3y 2 X b Dx 2y Y 2 3 b Dy 0 Admits An Integrating Factor Which Is A Function Of X Y 2 Mathematics Stack Exchange



Solved Solve The System X 2 Y 2 15 Xy 5 Y 0 Select One 5 5 2 5 5 2 B 5 5 2 5 5 2 C This System Is Dependent D No So Course Hero
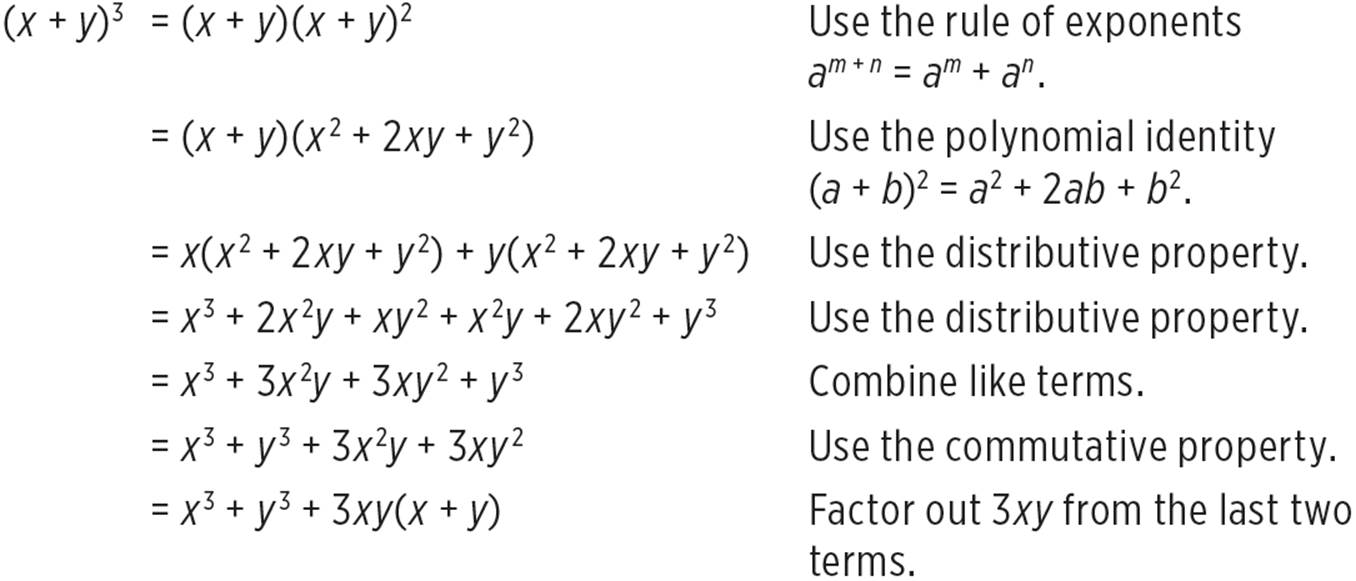



Polynomial Identities Complex Numbers And Polynomials High School Algebra Ii Unlocked 16



If Math X 2 Xy Y 2 A 2 Math How Will You Prove That Math Dfrac D 2y Dx 2 Dfrac 6a 2 X 2y 3 0 Math Quora




Algebraic Identities Of Polynomials A Plus Topper



Identity Vs Equation Acute Angel



1




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange




The Pythagorean Triple 5 12 13 Can T Be Generated From The Identity X 1 2 2x 2 X2 Brainly Com




How Do I Prove That X 2 Y 2 X Y 2 2xy Geometrically Intuitively Mathematics Stack Exchange



Simplify Each Of The Following Expressions I X Y Z 2 X Y 2 2 3 2 X 2 Y 3 Z 4 2 Sarthaks Econnect Largest Online Education Community




Solutions To Implicit Differentiation Problems




If X 2 Y 2 49 And X Y 3 Then Find The Value Of X 3 Y 3




Get The Right Pair Of Algebraic Identities A B A X Y 2 1 X Y X2 Y2 Xy B X2 Y 2 2 Brainly In



How To Draw The Graph Of X 2 Y 2 2x 0 Quora




Solved Verify The Following Pythagorean Identity For All Chegg Com




Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange



Which Polynomial Equation Is A Valid Identity 1 Gauthmath



How To Prove X 2 Y 2 Xy If X Y X Y Quora




Complete The Proof Drag And Drop The Expression To Correctly Complete The Proof Of The Polynomial Brainly Com




View Question A Student Is Asked To Calculate The Pythagorean Triples For The Number 9 Using The Identity X2 Y2 2 2xy 2 X2 Y2 2 The




Find The Product X 2y 3 X 2 4y 2 2xy 6y 3x 9 Youtube
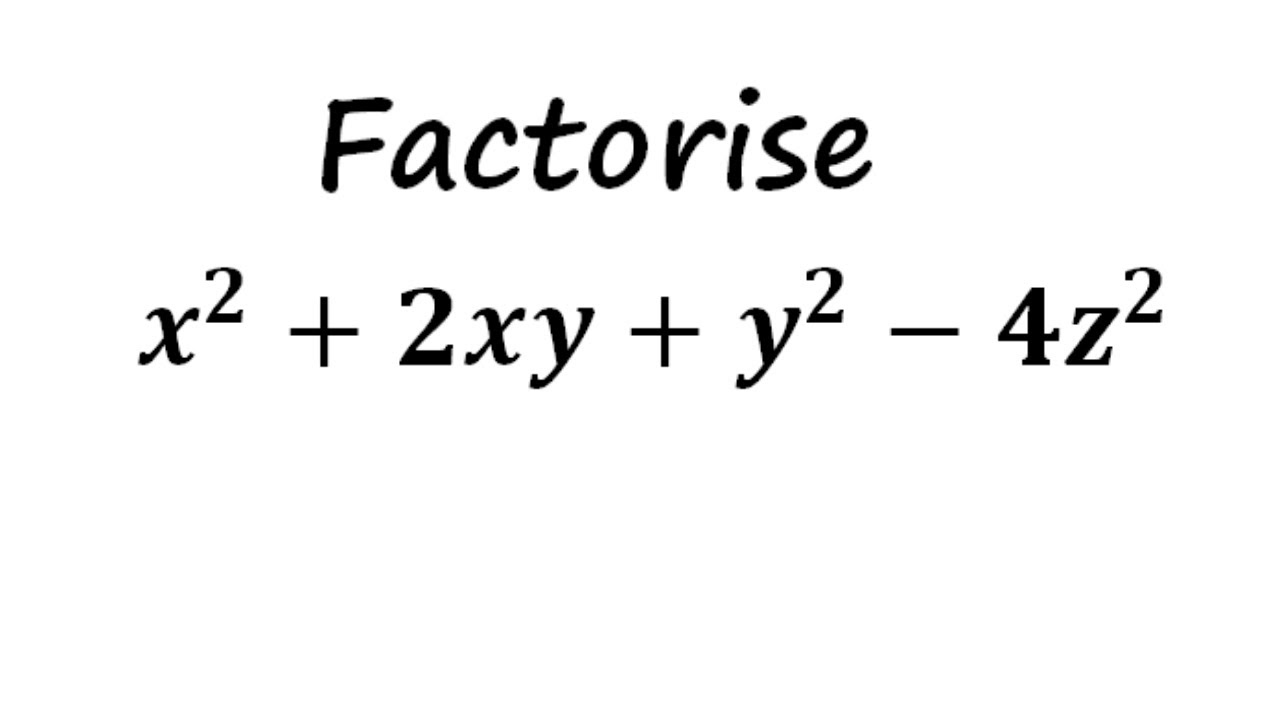



Factorise X 2 2xy Y 2 4z 2 Factorise X2 2xy Y2 4z2 Youtube



Prove X 2 Y 2 2xy And X 2 Y 2 Z 2 1 3



How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora



Why Doesn T Math X Y 2 Math Equal Math X 2 Y 2 Math Quora



Whitman Edu




Solved 2 Catherine Was Proving That X2 Y2 2 2xy 2 Chegg Com
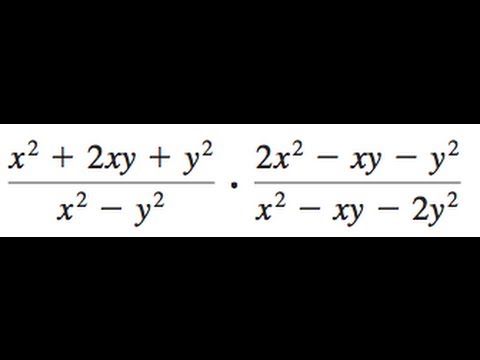



X 2 2xy Y 2 X 2 Y 2 2x 2 Xy Y 2 X 2 Xy 2y 2 Youtube




Product X 2 2y X 2 4 Xy 4y 2 Brainly In



How Do We Solve X 2 Y 2 10 1 X 1 Y 4 3 Quora




The Vector Field Of The Flow L X Is Given By X 2 2xy Y 2 2xy Download Scientific Diagram




Polynomials Ppt Video Online Download



How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8
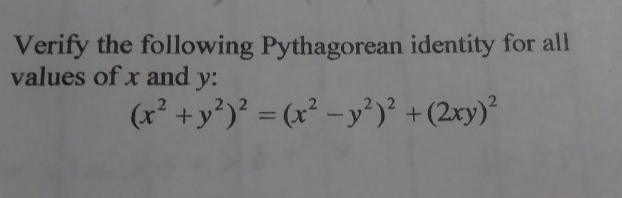



Solved Verify The Following Pythagorean Identity For All Chegg Com
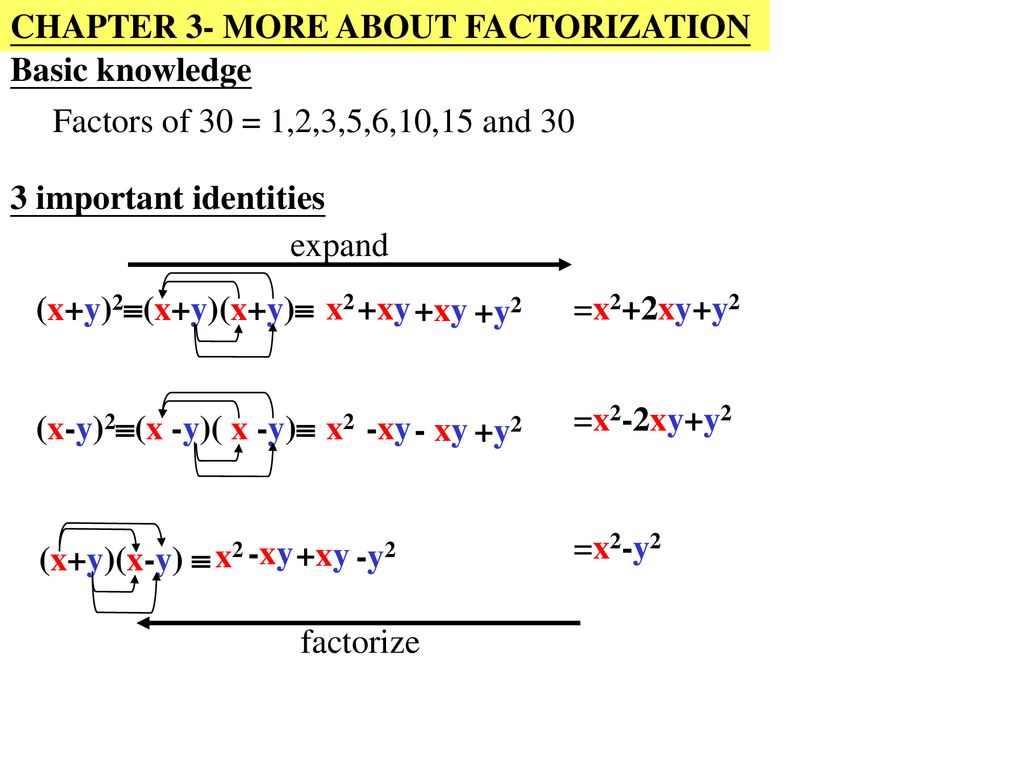



Chapter 3 More About Factorization Ppt Download




Expand And Simplify Binomial Squares 2x 3y 2 Youtube




Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange




Log X Y 2xy Detailed Login Instructions Loginnote




Find The Minimum Value Of 9x 2 2y 2 8xy 6x 11 Mathematics Stack Exchange




Expand 4x 2y 3z 2 Using Identity Brainly In
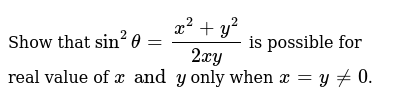



Darius Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show T




Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8




How Do I Prove That X 2 Y 2 X Y 2 2xy Geometrically Intuitively Mathematics Stack Exchange



X2 2xy Y2 Graph




Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange




Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube




Use An Identity To Factor X2 2xy Y2 1 Maths Polynomials Meritnation Com




Multiply X 2 4y 2 Z 2 2xy Xz 2yz By X 2y Z




Will Give 5 Stars Marshall Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show That 8 Brainly Com



1



How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora




Given X 2 Y 2 74 And Xy 35 Find The Value Of X Y And X Y




Solved Find The Volume Of The Solid Whose Base Is The Region Chegg Com



0 件のコメント:
コメントを投稿